സമഭുജ ത്രികോണം
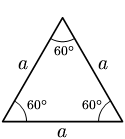
മൂന്നു വശങ്ങളും മൂന്നു കോണളവുകളും തുല്യമായ ത്രികോണങ്ങളാണ് സമഭുജ ത്രികോണങ്ങള്‍. ആയതിനാല്‍ ഓരോ കോണളവും 60 ഡിഗ്രീ വീതമായിരിയ്ക്കും.
ഒരു വശം a യും ലംബശീര്‍‌ഷം h ഉം തന്നിരുന്നാല്‍ സമഭുജത്രികോണത്തിന്റെ വിസ്തീര്‍‌ണ്ണം കാണുന്നതിന് 
എന്ന സൂത്രവാക്യം ഉപയോഗിയ്ക്കുന്നു.
a വശമായുള്ള സമഭുജത്രികോണം ആധാരമാക്കി വരയ്ക്കുന്ന:
- rആരമായുള്ള അന്തര്‍‌വൃത്തത്തിന്റെ വിസ്തീര്‍‌ണ്ണം
എന്ന സൂത്രവാക്യം ഉപയോഗിച്ചും - <math>R\,</math> ആരമായുള്ള പരിവൃത്തത്തിന്റെ വിസ്തീര്‍‌ണ്ണം <math>\pi R^2\,</math> അഥവാ <math>\frac{1}{3} \pi a^2</math> എന്ന സൂത്രവാക്യം ഉപയോഗിച്ചും കണ്ടെത്താം.
നിര്മ്മിതി
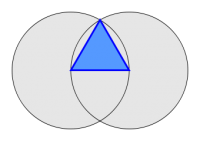
ആരമായുള്ള ഒരു വൃത്തം നിര്‍‌മിയ്ക്കുക. ഇതേ ആരത്തില്‍ തന്നെ കോം‌പസ്സുപയോഗിച്ച് വേറൊരു വൃത്തം നിര്‍മ്മിച്ച്, വൃത്തകേന്ദ്രങ്ങളേയും വൃത്തങ്ങള്‍ തമ്മില്‍ സന്ധിയ്ക്കുന്ന ബിന്ദുക്കളേയും യോജിപ്പിച്ചാല്‍ സമഭുജത്രികോണം ലഭിയ്ക്കും.