"സമഭുജ ത്രികോണം" എന്ന താളിന്റെ പതിപ്പുകൾ തമ്മിലുള്ള വ്യത്യാസം
ദൃശ്യരൂപം
No edit summary |
No edit summary |
||
| (മറ്റൊരു ഉപയോക്താവ് ചെയ്ത ഇടയ്ക്കുള്ള 11 നാൾപ്പതിപ്പുകൾ പ്രദർശിപ്പിക്കുന്നില്ല) | |||
| വരി 1: | വരി 1: | ||
[[ | [[Image:Triangolo-Equilatero.png|right|സമഭുജ ത്രികോണം]] | ||
മൂന്നു [[വശം|വശങ്ങളും]] മൂന്നു [[ | മൂന്നു [[വശം|വശങ്ങളും]] മൂന്നു [[കോൺ|കോണളവുകളും]] തുല്യമായ [[ത്രികോണം|ത്രികോണങ്ങളാണ്]] '''സമഭുജ ത്രികോണങ്ങൾ'''. ആയതിനാൽ ഓരോ [[കോണളവ്|കോണളവും]] 60 ഡിഗ്രീ വീതമായിരിയ്ക്കും. | ||
ഒരു [[വശം]] | ഒരു [[വശം]]'' a'' യും [[ലംബശീർഷം]] ''h'' ഉം തന്നിരുന്നാൽ സമഭുജത്രികോണത്തിന്റെ [[വിസ്തീർണ്ണം]] കാണുന്നതിന് [[Image:Snapshot1.png]] എന്ന [[സൂത്രവാക്യം]] ഉപയോഗിയ്ക്കുന്നു. | ||
''a'' വശമായുള്ള സമഭുജത്രികോണം ആധാരമാക്കി വരയ്ക്കുന്ന: | |||
* | * ''r''[[ആരം|ആരമായുള്ള]] [[അന്തർവൃത്തം|അന്തർവൃത്തത്തിന്റെ]] [[വിസ്തീർണ്ണം]] [[Image:Snapshot2.png]] എന്ന [[സൂത്രവാക്യം]] ഉപയോഗിച്ചും | ||
* | * ''R''ആരമായുള്ള [[പരിവൃത്തം|പരിവൃത്തത്തിന്റെ]] [[വിസ്തീർണ്ണം]] [[Image:Snapshot3.png]] എന്ന [[സൂത്രവാക്യം]] ഉപയോഗിച്ചും കണ്ടെത്താം. | ||
== | == നിർമ്മിതി == | ||
[[ | [[Image:340px-Equilateral_triangle_construction.svg.png|200px|thumb|left|സമഭുജ ത്രികോണത്തിന്റെ നിർമ്മിതി]] | ||
[[ആരം|ആരമായുള്ള]] ഒരു [[വൃത്തം]] | [[ആരം|ആരമായുള്ള]] ഒരു [[വൃത്തം]] നിർമിയ്ക്കുക. ഇതേ [[ആരം|ആരത്തിൽ]] തന്നെ [[കോമ്പസ്|കോംപസ്സുപയോഗിച്ച്]] വേറൊരു [[വൃത്തം]] നിർമ്മിച്ച്, [[വൃത്തകേന്ദ്രം|വൃത്തകേന്ദ്രങ്ങളേയും]] വൃത്തങ്ങൾ തമ്മിൽ സന്ധിയ്ക്കുന്ന ബിന്ദുക്കളേയും യോജിപ്പിച്ചാൽ സമഭുജത്രികോണം ലഭിയ്ക്കും. | ||
[[ | [[വർഗ്ഗം:ഗണിതം]] | ||
[[ | [[വർഗ്ഗം:ജ്യാമിതി]] | ||
<!--visbot verified-chils-> | |||
10:22, 26 സെപ്റ്റംബർ 2017-നു നിലവിലുള്ള രൂപം
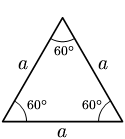
മൂന്നു വശങ്ങളും മൂന്നു കോണളവുകളും തുല്യമായ ത്രികോണങ്ങളാണ് സമഭുജ ത്രികോണങ്ങൾ. ആയതിനാൽ ഓരോ കോണളവും 60 ഡിഗ്രീ വീതമായിരിയ്ക്കും.
ഒരു വശം a യും ലംബശീർഷം h ഉം തന്നിരുന്നാൽ സമഭുജത്രികോണത്തിന്റെ വിസ്തീർണ്ണം കാണുന്നതിന്  എന്ന സൂത്രവാക്യം ഉപയോഗിയ്ക്കുന്നു.
എന്ന സൂത്രവാക്യം ഉപയോഗിയ്ക്കുന്നു.
a വശമായുള്ള സമഭുജത്രികോണം ആധാരമാക്കി വരയ്ക്കുന്ന:
- rആരമായുള്ള അന്തർവൃത്തത്തിന്റെ വിസ്തീർണ്ണം
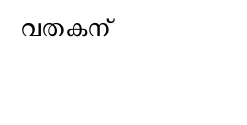 എന്ന സൂത്രവാക്യം ഉപയോഗിച്ചും
എന്ന സൂത്രവാക്യം ഉപയോഗിച്ചും - Rആരമായുള്ള പരിവൃത്തത്തിന്റെ വിസ്തീർണ്ണം
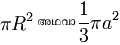 എന്ന സൂത്രവാക്യം ഉപയോഗിച്ചും കണ്ടെത്താം.
എന്ന സൂത്രവാക്യം ഉപയോഗിച്ചും കണ്ടെത്താം.
നിർമ്മിതി
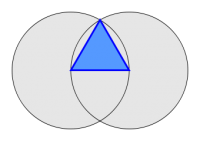
ആരമായുള്ള ഒരു വൃത്തം നിർമിയ്ക്കുക. ഇതേ ആരത്തിൽ തന്നെ കോംപസ്സുപയോഗിച്ച് വേറൊരു വൃത്തം നിർമ്മിച്ച്, വൃത്തകേന്ദ്രങ്ങളേയും വൃത്തങ്ങൾ തമ്മിൽ സന്ധിയ്ക്കുന്ന ബിന്ദുക്കളേയും യോജിപ്പിച്ചാൽ സമഭുജത്രികോണം ലഭിയ്ക്കും.
